72の法則とは?資産を2倍にする”時間”と”金利”が簡単に分かる計算式!

「72の法則」とは、お金が2倍になるまでの金利と年数の関係を表した式です。
2倍になる「年数」を知りたい場合は
72÷金利=お金が2倍になる期間(年) ※おおよそ
で求められます。
この式を使えば「いつまでに」「どれくらい」のお金になるか(増えるか)が分かります。
また、借入れ・ローン時にも応用することができ、「借金がどの程度の期間で2倍になるか」も知ることができます。(詳しくは 2-2 でご紹介いたします。)
この記事では、具体例をたくさん交えながら、72の法則の使い方を詳しく説明していきます。
※資産運用において重要な言葉、「単利」「複利」についても分かりやすく説明していますので併せて読んでみてください。
72の法則は、お金が2倍になる期間と金利がわかる便利な式!
冒頭でも書いた通り、72の法則は、お金が2倍になる金利と期間の関係を表した法則です。
元々は、
金利(%)× お金が2倍になる期間(年)=72
となることから、この式を変形すると以下の式になります。
<お金を2倍にするために必要な年数表>
| 金利 (利回り・利率) |
計算式 | 2倍に必要な年数 (近似値) |
| 1% | 72÷1=72 | 72年 |
| 2% | 72÷2=36 | 36年 |
| 3% | 72÷3=24 | 24年 |
| 4% | 72÷4=18 | 18年 |
| 5% | 72÷5≒14 | 14年 |
| 6% | 72÷6=12 | 12年 |
| 7% | 72÷7≒10 | 10年 |
| 8% | 72÷8=9 | 9年 |
| 9% | 72÷9=8 | 8年 |
| 10% | 72÷10≒7 | 7年 |
また、さらに式を変形させることで「お金が2倍になる金利」も求めることができます。
| ※注意 なお、この72の法則で出した数字は、近似値を簡易的に出す法則です。あくまで、目安としてご使用ください。 |
では、さっそく使い方を見てみましょう。
72の法則の使い方【具体例付き】
お金が2倍になる期間が分かる、2倍になる金利が分かる
先ほどの式を変形すると以下の式になります。
お金が2倍になる期間が知りたければ、72をその金利(資産運用であれば、運用で得られる利率、利回り)で割ればよい、ということです。
金利3%で毎年運用した場合、お金が200万円になるまで、約24年必要。
(※2018年現在、金利0.01~0.1%程度)
金利0.1%で銀行に預け続けると、お金が200万円になるまで、約720年必要。
(現在の銀行の金利では、お金が増えないことがよくわかります。)
一方、先ほどの式で、お金が2倍になる期間(年)を入れると、逆に、2倍になる金利を求めることができます。
先ほどの逆で、24年間かけるのであれば、お金が200万円になるまで約3%で運用し続ければよい、ということが分かる。
実際にこの式を使うケースを考えると、おそらくもっと早く、〇年で2倍にするにはどれくらいの金利が必要か?を計算するケースが多いでしょうか。
10年で2倍にするためには、毎年7.2 %で運用しなければならないことが分かります。運用のハードルがぐっと上がりますね。
ここまでの話で、資産運用においては、金利と時間の関係が重要だということが分かりました。次に、お金を借りる場合には、どのように72の法則が役に立つのかを見てみましょう。
借金やローンであれば、借入金額が2倍になってしまう期間が分かる
72の法則の計算式は、借金や借入れ、ローンにも同じように当てはめて、「借金がどの程度の速さで2倍になるか」が分かります。先ほどの例で考えてみましょう。
(※同一条件で計算するために、あくまで返済をまったく行わなかった場合のシミュレーションとして見ておいてください。実際の借り入れの場合は、毎月返済していくのでここまでにはなりません。)
約24年間(無返済で)借りると、返す金額が2倍に。
これが2%であれば、72÷2%=36年で2倍という計算になり、12年もの差が出ます。
このケースでは100万円ですが、例えばもっと金額が大きくなる住宅ローンで、このように長期にわたる借り入れを行う場合、少しの金利の違いが非常に大きな金額差を生み出していく、ということが分かります
これを金利の高いサービス、たとえばクレジットカードのリボ払い(年利15%程度)や分割払い(年利8~18%程度)、キャッシング(年利15%〜18%程度)に当てはめていくと、これらの返済負担が非常に重いことが分かりますね。
72の法則は、お金が2倍になるまでの金利と期間の関係を表した法則でした。72の代わりに115を使うと、まったく同じように、お金が「3倍」になる期間や金利を計算できます。
金利(%)× お金が3倍に倍になる期間(年)= 115
それぞれ変形すると、以下のようになります。
お金が3倍になる期間 (年) = 115 ÷ 金利(%)
金利(%) = 115 ÷ お金が3倍になる期間 (年)
合わせて使ってみてくださいね。
72の法則は「複利」の場合であることに注意!
「複利」と「単利」の違いは、利息の付き方
実は、金融商品には「単利・複利」があるのですが、今までご説明した72の法則は、「複利」で運用した場合の計算式です。実際の資産運用の際にこの計算式を当てはめるなら、複利の商品で運用していることが前提になります。
そこで、この章では「単利・複利」について解説します。2つの違いは、「利息の扱い方」です。資産運用の基本的な知識ですので、まずは定義だけ簡単に理解しておきましょう。
「単利」とは、
当初預けた元本に対してのみ利息がつきます。利息を再運用することはしません。
<単利の増え方> 元本100万円を、年利7%で運用した場合
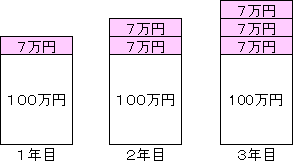
「複利」とは、
当初預けた元本についた利息をどんどん元本に組み入れて新たな元本とし、利息を再運用する方法です。利息が元本に組み込まれ、元本自体が大きくなっていきますので、その様子をたとえて、よく「雪だるま式に増える」などと表現されます。
<複利の増え方> 元本100万円を、年利7%で運用した場合
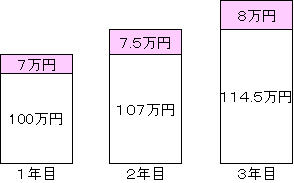
運用している商品が複利の商品か、単利の商品かで、元本額が変わってくるイメージがつきましたでしょうか?さらに、時間を経た時の差を見てみます。
単利と比べると、圧倒的に複利が有利!
100万円を7%で40年間運用した場合の、単利と複利の受取額を比較してみましょう。
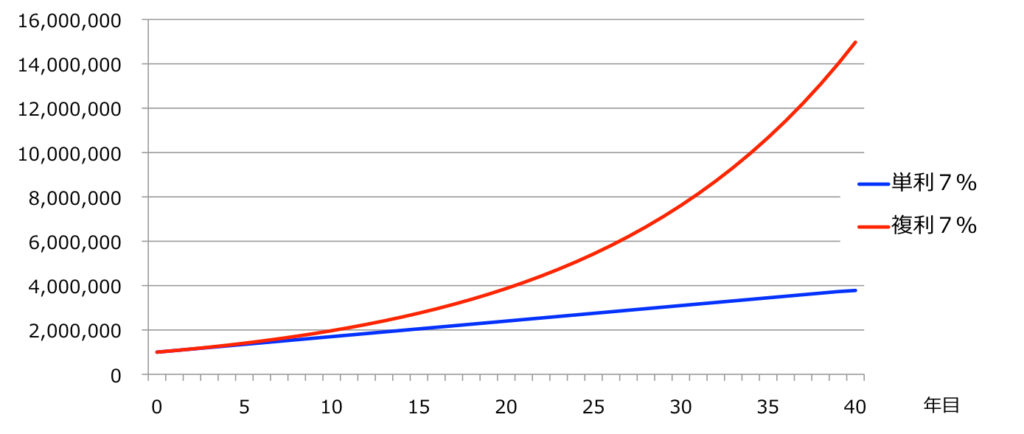
単利の場合、
7万円の利息 x 40年 = 280万円
で元利合計(元本と利息を合わせた合計)は380万円に過ぎません。(約3.8倍)
一方で、
複利の場合、
10年を過ぎたあたりから差がつき始め、
利息部分が13,974,458円、元利合計で14,974,458円に増えています。(約14.9倍)
複利の方が得なことがよくわかりますね。
また、資産を倍にするために必要な年数を、複利と単利で、運用利回り別にまとめたのが以下の表です。
| 金利 (運用利回り・利率) | 複利 | 単利 |
| 1% | 72年 | 100年 |
| 2% | 36年 | 50年 |
| 3% | 24年 | 33年 |
| 5% | 14年 | 20年 |
| 6% | 12年 | 17年 |
やはり利回りにかかわらず、複利が有利なことが分かります。金融商品を選ぶ際には、金利だけでなく、単利か複利かの利息自体の付き方にも興味をもっていただければと思います。
なお、上記のように単利の場合を計算するには、「110の法則」を使います(こちらもすべて近似値です)。
「単利」で、お金が2倍になる期間と金利がわかる「110の法則」
金利(%)× お金が2倍になる期間(年)=110
単利と複利について、また具体的には、どんな商品がそれにあたるのかをより詳しく知りたい方、複利の効果を最大にする方法については、こちらの記事も参考にしてみてください。
まとめ - 72の法則を使って、お金を増やそう
現在の低金利下では、定期預金で年利0.1%運用をした場合、倍の200万円にするのに約720年(=72÷0.1)の投資期間がかかる一方、年利3%で運用した場合には約24年(=72÷3)で倍になります。
また、これは物価上昇(インフレ)を考慮していない場合の話で、物価が上がると、同じ金額でも買えるものが減ってしまいます。結果として、実質、お金が減っているのと同じ効果が起こります。
解説したとおり、72の法則で時間と金利(利回り)の関係に注目すると、なるべく長期間をかけることで、無理のない利回りで2倍が実現できるということが分かりました。重要なのは、「複利の力を利用しつつ、長期投資をすること」で、それにより成果が安定しやすくなります。また、そのためには早く始めることもポイントになるといえるでしょう。
投資にリスクを感じている方にも、「何もしないことのリスク」を加味しつつ、リスクをコントロールした運用を検討することをお勧めしたいと思います。資産運用の基本について、参考になる記事をご紹介しますので、ぜひ合わせて読んでみてください。
資産運用の世界に踏み込むために!主な用語と知っておきたい基本を解説










