利息のつき方は2種類ある！複利の商品を使って上手に資産を増やそう
基本的に金融商品は、利益の付き方が「単利」か「複利」のどちらかです。結論から言うと、「複利」の方が得なのですが、資産運用を始めている多くの人は、自分の購入している商品が「単利」なのか「複利」なのかということすら知りません。
それは、おそらく、金融商品を購入するときに「この商品は単利と複利のどちらなのか？」ということを考えていないからか、または、そもそも、「単利」と「複利」の違いがわからないかです。
その結果、例えば、投資信託を購入している人の多くが「単利」の商品を選んでいるというのが現状です。
この記事では、「単利」と「複利」の違いを解説するとともに、「複利」の力の活かし方、「複利」の金融商品を紹介します。
アインシュタインが「人類における最大の数学的発見」（諸説あり）と言っている「複利」の力を上手に活用して、お金を増やしていきましょう。
単利と複利
単利と複利の違い
「単利」とは、当初預けた元本に対してのみ利息がつきます。利息を再運用することはしません。
「複利」はこれとは異なり、当初預けた元本についた利息をどんどん元本に組み入れて新たな元本とし、利息を再運用する方法です。このため、利息が元本に組み込まれ、元本自体が大きくなっていきますので、その様子をたとえて、よく「雪だるま式に増える」などど表現されます。
具体的な数字で見てみましょう。
＜単利の増え方＞ 元本１００万円を、年利７％で運用した場合
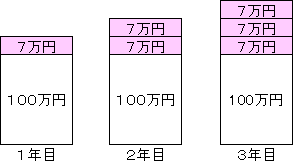
＜複利の増え方＞ 元本１００万円を、年利７％で運用した場合
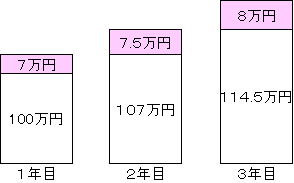
単利と複利を比べると３年目では、複利の方が約１.５万円も得をすることになりますね。この差が積み重なると、雪だるま式に差が出てくるのです。
100万円を7％で40年間運用した場合の、単利と複利の受取額を比較してみましょう。
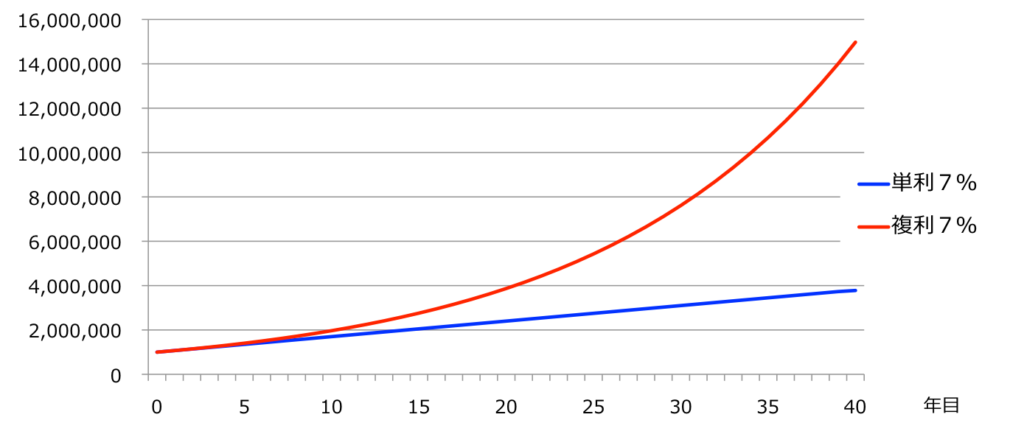
単利の場合、7万円の利息ｘ40年＝280万円で元利合計（元本と利息を合わせた合計）は380万円に過ぎません。（約3.8倍）
一方、複利の場合、10年を過ぎたあたりから差がつき始め、利息部分が13,974,458円、元利合計で14,974,458円に増えています。（約14.9倍）
複利の方が得なことがよくわかると思います。
単利の金融商品、複利の金融商品の例
実は金融商品も、単利の商品と複利の商品があるのを知っていますか？
普段あまり意識していないことが多いと思いますが、具体的な商品の例を挙げておきます。
| 単利商品 | 複利商品 |
| 定期預金（銀行） 毎年利払型 債券（国債、地方債、社債等） 投資信託（毎月分金配受取型）※１ | 定額貯金（ゆうちょ銀行） 定期預金3年超 元利自動継続型 投資信託（無分配型、分配金再投資型）※１ 貯蓄型保険 |
言うまでもなく、中長期的な運用を考えている場合には、複利の商品を選ぶほうが有利なのですが、そのポイントを考慮せずに選んでいるケースも多いのではないでしょうか。定期預金のように長期で安定運用をしたいと思っているお金こそ、かなりもったいないことをしている可能性があるかもしれません。
※１ 注意！ 投資初心者を含む、多くの人に人気の毎月分配型の投資信託も単利の商品です。
こちらも同じ理由で、長期運用を目指すべき若い人や現役世代にはあまりお勧めできません。資産形成の途中である現役世代にまで分配型を積極的に販売する金融機関については、金融庁も問題視しています。
毎月分金配受取型の投資信託が長期投資に向かない理由は、以下の記事で詳しく解説していますので、当てはまる人、検討している人は、ぜひ参考にしてみてください。
投資信託は『分配型』に注意！分配金受け取りのメリットデメリット
複利の効果
複利は「時間の力」を利用し、投資による利益を元本に加えて、さらに価値を増加させていきます。この合計金額が、再度投資に回されて更なる利益を生んでいくことになります。
複利の特長
- 同じ金額であれば、単利よりもずっと効果的に増やすことができる。また少額であっても効果は変わらない。
- 効果を得るために必要なものは時間だけ。追加でコストがかかったり、リスクを取ったりする必要はない。
時間さえかければそのメリットを得られるため、複利の活用は、特に若い人にお勧めです。例えば毎月の積立て、引き落としなどによる定期的な継続投資を行うことは、複利の効果を活用する一つの方法です。
毎月定額引き落としは、元手の少ない人でも実行しやすいため、よく選択される方法です。
また、複利で、金利がいくらか分かれば、何年で元本が2倍になるかを簡単に割り出せる式もあります。「7２の法則」です。
「7２の法則」
元本が2倍になる期間（年）＝ 72 ÷ 金利（年利・％）
※ただし、この式で割り出せる数字は、あくまでも近似値です。
ざっくり計算すると、元本が2倍になるのに必要な年数は、金利ごとに以下のようになります。
| 運用する金利 | 計算式 | 2倍になるのに必要な年数 |
| 1% | 72÷1=72 | 約72年 |
| 3% | 72÷3=24 | 約24年 |
| 5% | 72÷5=14 | 約14年 |
| 7% | 72÷7=10 | 約10年 |
| 10% | 72÷10=7 | 約7年 |
また、式を変形すれば、逆に元本を倍にするために必要な金利を割り出すこともできます。
たとえば、「手持ちの資金を5年で2倍にするためには、何％で運用しなければならないか」という問いには、
72 ÷ ５年 ＝ 年利14％
と答えられます。
７２の法則については、使い方を含め、以下の記事で詳しく解説していますので、参考にしてみてください。
72の法則とは？資産を2倍にする”時間”と”金利”が簡単に分かる計算式！
複利の効果を最大にするには、「時間」を掛けることと、「金利」が必要です。
最低でも10年以上、長期で続けることが重要です。途中でやめざるを得なくならないように、自分のライフプランを考えて、余剰資金で行うことがポイントです。また、長期で続けるためには、言うまでもなく早く始めれば始めるほど有利です。
ただし、金利が低すぎる時は効果が小さくなってしまいます（例えば、現在の定期預金0.01％では、100万円を預けても4,000円しか増えません）。
金利を得るためには、預貯金で積み立てるのではなく、資産運用することがが必要となってきます。
まとめ
複利を利用した中長期的な資産運用は、年金やインフレのように、将来的にじわじわ効いてくるリスクへの備えとして有効な手段です。
特に20－30代の若い世代は、時間をかけて資産形成をできる強みがあります。計画的にマネープランを検討する必要性が高まっていますので、ぜひ、効率的、有利に資産を増やす方法を知り、活かしていただきたいと思います。
普段あまり意識していない人も多いと思いますが、普通預金を含め、金融商品には単利の商品と複利の商品があります。すでに持っている金融商品・資産があるのであれば、まずはぜひ、その点を意識して運用を見直してみましょう。
お金に関する相談ならなんでもOK！
お家でも、店頭でも◎
相談内容はお金に関することならどんな内容でもOK！相談はオンラインでも来店でも可能です。相談内容に合わせて適切なファイナンシャルプランナーを紹介いたします。
お休みなどご都合に合わせて
希望の日程で相談可能！
お急ぎの方は最短即日のご相談予約も可能！１回の相談で相談しきれないお悩みは“何度でも”無料で相談できるので、初めての方でも、お悩みがたくさんある方でも安心です。
